The paper
In this blogpost, we’ll explore the paper: Mamba: Linear-Time Sequence Modeling with Selective State Spaces, which introduced a neural network architecture that bridges the gap between RNNs and Transformers.
The authors: Albert Gu and Tri Dao, are well-known for their contributions to the FlashAttention, which significantly improved Transformer efficiency and have been widely adopted in all prominent deep learning libraries. These researchers clearly have deep experience in optimizing large sequence models.
Motivation
In the paper authors argue that:
A fundamental problem of sequence modeling is compressing context into a smaller state
According to their statement, the biggest problem of Transformer architecture is the fact that it explicitly doesn’t compress the context at all. Each new token processed by transformer need to attend with all previous tokens, resulting in quadratic compute and memory cost with respect to sequence length.
On the other hand RNNs compress all history into a fixed-size hidden state,
updating it at each step. Calculating a single new token is constant as it is
independent of the current sequence length, which makes the cost of computing a
whole sequence linear with respect to its length.
Note: The fact that model’s memory is constant doesn’t mean it is
small it is capable of giant compute but is not constrained by sequence
length
The Transformer architecture shines when it comes to training as Attention is easy to parallelize. RNNs are much more problematic in this regard as you need to perform each step sequentially in order to perform backpropagation.
It would be perfect to combine the training time performance of transformers and RNN type inference. That’s where State Space Models (SSMs) and later Mamba come in.
SSM - State Space Models
SSMs originate from control theory, where they describe how a physical system evolves over time. The key insight is that the same math can model sequences in deep learning, letting us express how an internal state changes in response to inputs:
Continuous SSMs
The State Space Model can be defined by the following differential equation: $$ \begin{aligned} \frac{d}{dx}h(t) &= \textbf{A}h(t) + \textbf{B}x(t) \\ y(t) &= \textbf{C}h(t) \end{aligned} $$
Where:
- $h(t)$ - hidden state at time t
- $x(t)$ - input at time t
- $y(t)$ - output at time t
- $A$ -defines how old hidden states influence new ones
- $B$ - defines how inputs influence the hidden state
- $C$ - maps the internal state to output Notes:
- $A$, $B$, $C$ are constant in time (linear time-invariant system)
- The output $y(t)$ depends on the input $x(t)$ only through the hidden state $h(x)$
- You can think about $A$ kind of like about a forget gate in LSTMs
Solving the differential equation
Solving the system gives: $$ h(t) = e^{At}h_0 + \int_0^t e^{A(t-\tau)} Bx(\tau) d\tau $$ and thus: $$ y(t) = Ce^{At}h_0 + \int_0^t Ce^{A(t-\tau)} Bx(\tau) d\tau $$ Notice that the second term is convolution between the input $x(\tau)$ and a kernel defined by $Ce^{A(t-\tau)}B$ This is great news as convolution operations are easy to parallelize on GPUs.
Discretization
In order to implement this in practice we need discrete version. Let’s say we update the system every $\Delta$ seconds, then: $$ \begin{aligned} h_{k+1} &= \overline{A}h_k + \overline{B}x_k \\ y_k = Ch_k \end{aligned} $$ Here $\overline{A}$ and $\overline{B}$ are discrete equivalents of $A$ and $B$, and they are commonly obtained through exponential mapping:
$$ \begin{aligned} \overline{A} &= exp(\Delta A) \\ \overline{B} &= (exp(\Delta A) - I)A^{-1}B \end{aligned} $$
Because $\overline{A}$, $\overline{B}$, $\overline{C}$ remain constant over time, this system is said to be linear-time-invariant (LTI). That makes it equivalent to a linear recurrence or convolution, both of which can be computed in parallel
S4
A prominent example of this approach is the S4 model, which introduced carefully structured matrices to make SSMs both stable and scalable. However, while S4 demonstrated impressive efficiency, its parameters were fixed, which resulted in bad results inthe Selective Copying Task. The Selective State Space Models aim to remove that limitation by making parameters adaptive to the input.
Mamba: Selective State Space Model
Mamba extends SSMs by making them input-dependent, in other words selective. In Mamba, these matrices become functions of the current input: $$ \Delta_k = f_{\Delta}(x_k) \\ B_k = f_{B}(x_k) $$ This allows Mamba to dynamically adjust how much it updates or forgets the state depending on the data similar in spirit to the gating in LSTMs, but still preserving the efficiency of SSMs.
Here’s a simplified pseudocode version of Mamba’s update:
Δ = f_delta(x_k) # Input-dependent step size
B = f_B(x_k) # Input-dependent input projection
h = A_d(Δ) @ h + B @ x_k # State update
y = C @ h
Optimizations
Even though the parameters depend on the input, Mamba keeps the computation structured so that:
- It can still be parallelized (via convolution form) during training.
- It can still run recurrently (step-by-step) during inference
- Selectivity functions $\Delta_k$ and $B_k$ aim to be as lightweight as possible typically small linear projections
Hardware-Aware Algorithm
In order for some neural network architecture to succeed it needs to be efficient on the real hardware. Mamba is designed with modern GPUs in mind, building on ideas from FlashAttantion.
To maximize throughput, it uses a hardware-aware memory layout, which carefouly keeps hot data close to compute units:
- SRAM - Static Random Access Memory (small capacity, fast) - stores the hidden state
- HBM - High andwidth Memory (large capacity slow) - holds the sequence data
- CUDA kernels are fused so that data movement between SRAM and HBM (the real bottleneck on GPUs) is minimized
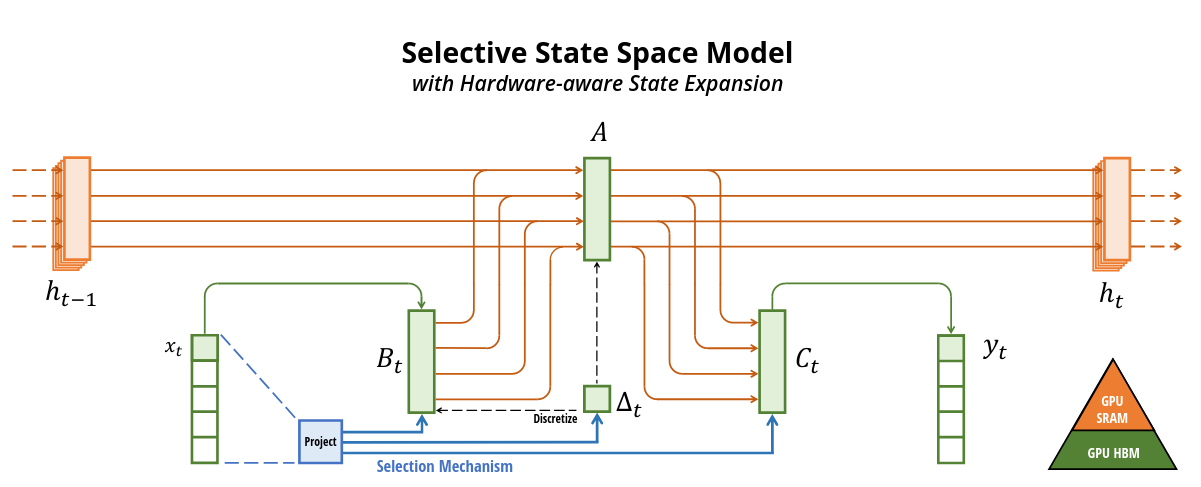
Below is the model architecture diagram taken from the original paper that
nicely connects most of the concepts that we talked about in this blogpost.
 Albert Gu and Tri Dao. 2024. Mamba: Linear-Time Sequence Modeling with
Selective State Spaces. In First Conference on Language Modeling.
Albert Gu and Tri Dao. 2024. Mamba: Linear-Time Sequence Modeling with
Selective State Spaces. In First Conference on Language Modeling.
Conclusions
Mamba represents a middle ground between Transformers and RNNs. It has shown impressive results across diverse domains: language modeling, DNA sequence analysis, and audio generation, achieving Transformer-level accuracy while significantly outperforming them in speed and scalability.
While models based on Mamba architecture look very promising, the research community continues to push the limits of Attention mechanisms, with modern Transformers handling context windows spanning millions of tokens. It is unclear then what is the future of sequence modelling, we might soon start seeing some hybrid models combinging the reasoning power of Transformers and efficiency of Mamba.
Further reading
Take a look at the follow up ICML paper of the same authors:
Transformers are SSMs: Generalized Models and Efficient Algorithms Through
Structured State Space Duality
To understand S4 better:
S4 - Efficiently Modeling Long Sequences with
Structured State Spaces
If you are a visual learner I cannot recommend enough the blog of Maarten
Grootendorst:
A Visual Guide to Mamba and State Space
Models
If you prefer video format here are some nice youtube videos about Mamba: